II.2. Représentation graphique des données
Après avoir obtenu un échantillon ou dénombré une population, on dispose le plus souvent de données numériques brutes présentées sous la forme d’une série de valeurs (dans le cas d’une VA quantitative) ou sous la forme d’un tableau donnant le nombre d’individu présentant un caractère qualitatif. Présentées ainsi, ces données sont rarement « parlantes » et il est nécessaire de dresser une représentation graphique afin de faire ressortir une partie de l’information. Suivant le type de variable aléatoire, le mode de représentation graphique va être différent.
2.1. VA qualitative
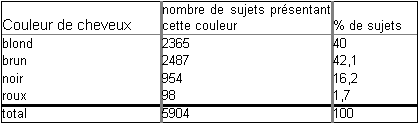
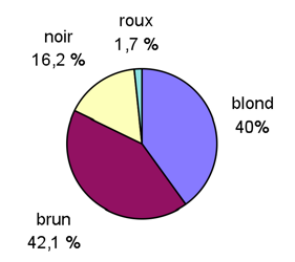
Le tableau suivant donne les On dispose alors de 4 classes ou nombre de personnes (effectif absolu) présentant une couleur donnée dans un échantillon. Ce tableau peut être représenté tel quel (en nombre) ou en pourcentage sur une graphique à secteur.
2.2. VA discrète (quantitative discontinue)
Ce type de variable est associée généralement à un diagramme en bâtons où l’axe horizontal des abscisses porte les valeurs prises par la VA (xi) tandis que l’axe vertical des ordonnées porte l’effectif absolu (ni) observé.
Si l’on s’intéresse au nombre de personnes à bord d’une voiture dans 2 villes différentes, on peut dresser le tableau suivant :
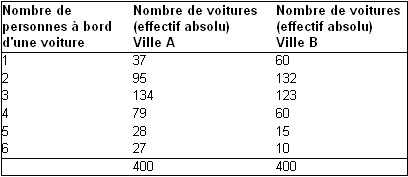
Le diagramme en bâtons correspondant est le suivant :
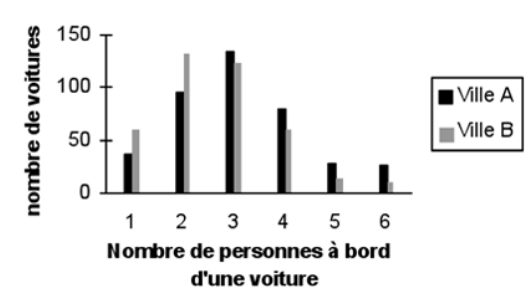
Ce type de représentation permet de mieux visualiser la distribution observée et semble indiquer que l’occupation des véhicules est plus importante dans la ville A que dans la ville B. Mais on ne peut faire confiance à cette affirmation simplement à la vue d’un graphique ; il faudrait une analyse statistique plus approfondie...
Un autre mode de représentation est le diagramme des fréquences cumulées.
La fréquence absolue est le nombre de répétition d’une valeur numérique.
Dans l’exemple précédent, fréquence absolue et effectif se confondent. En ajoutant à chaque effectif (dans une classe donnée) l’effectif précédent, on obtient les effectifs absolus cumulés qui se représentent graphiquement de la façon suivante :
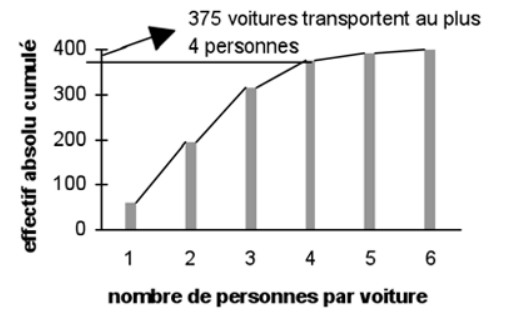
Le diagramme des fréquences cumulées permet la lecture du nombre de voiture transportant par exemple au plus 4 personnes dans la ville B.
Il est souvent intéressant de tracer le diagramme des fréquences relatives cumulées. Dans ce cas, l’effectif est exprimé en pourcentage. La lecture du graphique devient alors indépendante de la taille de l’échantillon.
2.3. VA quantitative continue
Dans le cas de ces variables, suivant la grandeur mesurée et la sensibilité de la méthode utilisée, il est fréquent d’obtenir autant de valeurs différentes que de données si bien que la représentation graphique n’a dans ces conditions aucun sens. On est donc généralement amené à regrouper les données en classes.
A la différence des VA discrètes, une classe donnée ne contient pas une seule valeur mais une infinité de valeurs possibles sur un intervalle défini (appelé intervalle de classe). Cet intervalle permet de définir également une amplitude de classe (différence entre les valeurs supérieure et inférieure de la classe). La valeur centrale de la classe est appelée centre de classe.
La répartition des données brutes en classes nécessite donc de la part du statisticien de faire un choix sur le nombre de classes et donc sur l’amplitude. Ce choix doit être suffisamment judicieux pour permettre la représentation graphique des données sans perdre pour autant trop d’information initialement contenue dans la série statistique.
C’est un ensemble de rectangles accolés ayant les caractéristiques suivantes :
-
la base de chaque rectangle correspond à l’amplitude d’une classe. Généralement toutes les classes d’une série statistique ont même amplitude.
-
la hauteur du rectangle est égale soit à l’effectif absolu (ou fréquence absolue) de la classe, soit à la fréquence relative (correspondant au rapport ni/n où ni est l’effectif absolu de la classe i et n l’effectif total de la série statistique). La surface de chacun des rectangles, si l’amplitude de classe est constante est alors proportionnelle à l’effectif de la classe
-
Il peut être intéressant de tracer l’histogramme des densités de fréquences. La densité de fréquence fxi correspond au rapport , où Δxi est l’amplitude de classe (ou base du rectangle). La surface d’un rectangle (fxi. Δxi ) dans cette représentation graphique est alors égale à la fréquence relative de la classe correspondante et la surface totale des rectangle est égale à 1 quelle que soit la distribution initiale On verra par la suite que l’on peut généraliser ce résultat à la distribution d’une variable continue.
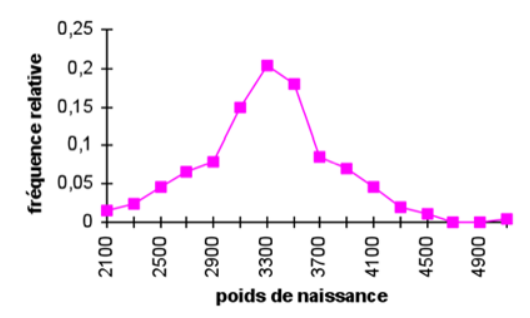
L’exemple suivant montre la distribution des poids de naissance de nouveau-nés dans une maternité (données extraites de : D. Schwartz, méthodes statistiques à l’usage des médecins et des biologistes, Médecine-Sciences, Flammarion 4ème ed. )
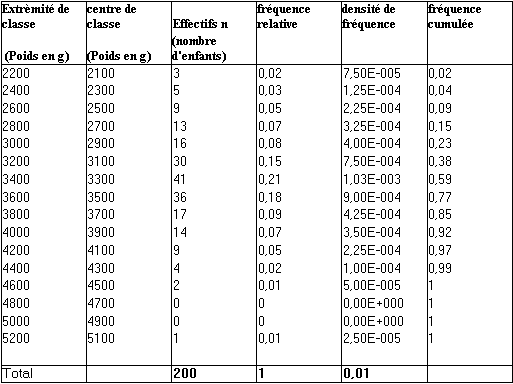
Dans cet exemple, toutes les classes ont même amplitude (200 g) et il y a au total 16 classes ce qui est un nombre suffisant pour représenter la distribution initiale (200 valeurs). On remarquera qu’une partie de l’information initiale a été perdue puisqu’à la vue du tableau il n’est plus possible de différencier les nouveau-nés d’une même classe.
A partir de ce tableau de valeurs, on peut tracer les histogrammes des effectifs absolus, des fréquences relatives et des densités de fréquence.
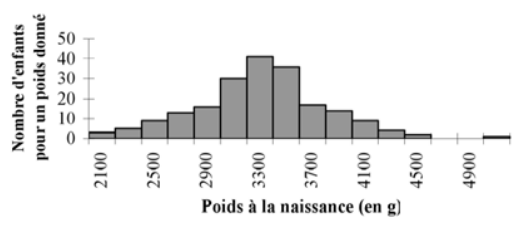
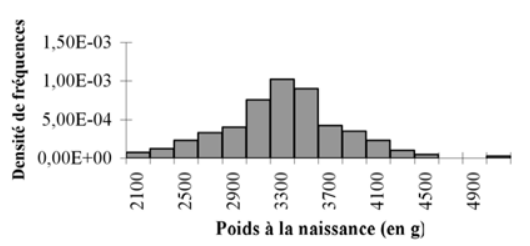
Le polygone des fréquences est représenté en joignant les milieux des cotés supérieurs des rectangles dans un histogramme. C’est une ligne brisée dont les extrémités rejoignent l’axe des abscisses.
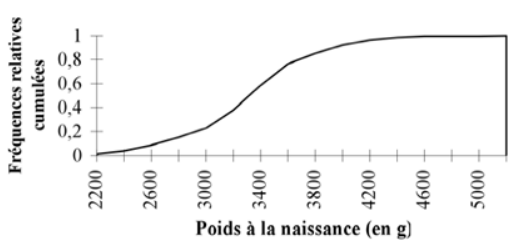
Ce type de courbe permet une lecture rapide du pourcentage de nouveau-nés dont le poids est compris entre deux valeurs. Il suffit de faire la différence entre les 2 ordonnées correspondant à l’intervalle de poids fixé.
2.4. Conclusion
La représentation graphique d’une série statistique est une étape très importante dans l’analyse d’un problème statistique car elle donne une information sur la forme de la distribution observée. Cette forme est souvent caractéristique, comme l’allure en cloche observée pour les histogrammes de poids des nouveau-nés. Nous verrons que cette allure en cloche caractérise la distribution d’un grand nombre de variable aléatoires.
Pour un échantillon donné, l’analyse graphique de la distribution, couplée à une étude statistique plus approfondie fournit une indication sur la distribution de la variable aléatoire dans la population d’où l’on a extrait l’échantillon.
Dans la démarche de qualité visant à maîtriser un processus industriel, cette approche permet de contrôler le procédé et de prédire les propriétés d'une fabrication. Ainsi, si la forme de la distribution ne varie pas d'un lot de fabrication à un autre, on dispose d'un élément positif pour démontrer la stabilité du processus.
Deux éléments, autres que la forme de la distribution apparaissent également lorsque l'on décrit graphiquement une série statistique. On remarque en effet que les valeurs se distribuent autour d'une valeur centrale avec un étalement (une dispersion) plus ou moins grand(e). L'analyse de ces deux paramètres, tendance centrale et dispersion, permettent de décrire de façon quantitative une distribution statistique.
